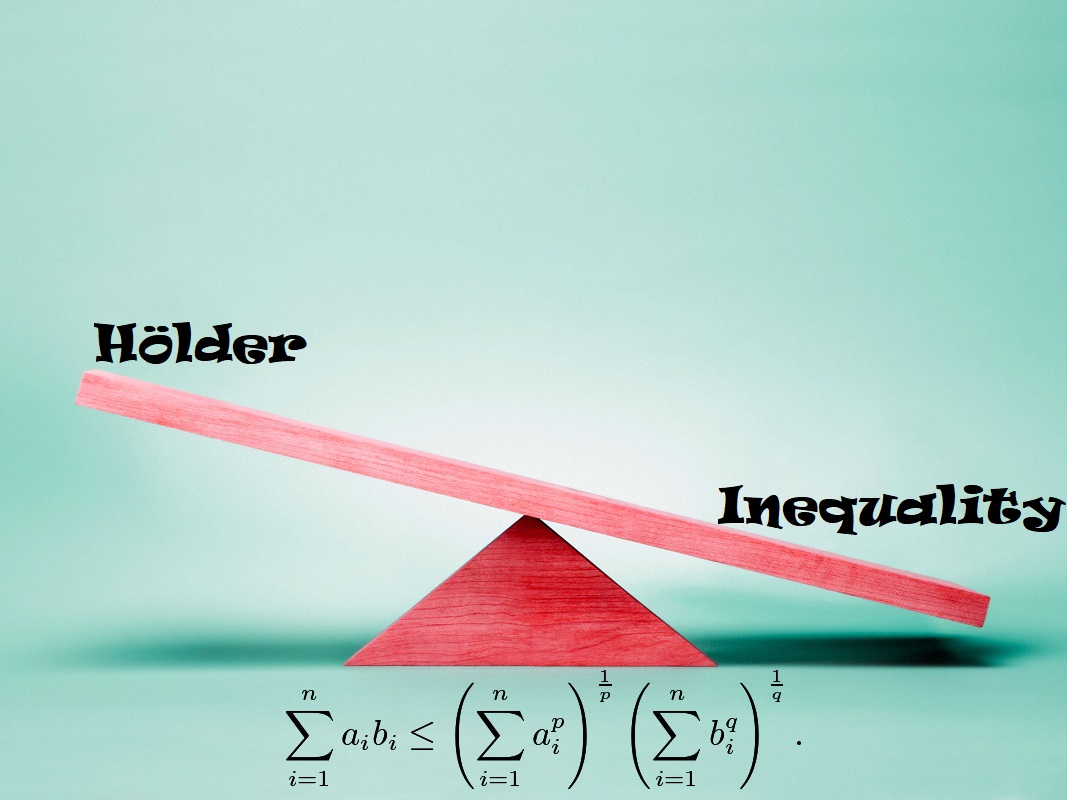
Holder Inequality Expectation . Then hölder's inequality for integrals states that. Prove that, for positive reals , the following inequality holds: what does it give us? Let 1/p+1/q=1 (1) with p, q>1. hölder’s inequality, a generalized form of cauchy schwarz inequality, is an inequality of sequences that generalizes multiple sequences and. (lp) = lq (riesz rep), also: Jensen’s inequality gives a lower bound on expectations of convex. How to prove holder inequality.
from blog.faradars.org
Let 1/p+1/q=1 (1) with p, q>1. Then hölder's inequality for integrals states that. How to prove holder inequality. hölder’s inequality, a generalized form of cauchy schwarz inequality, is an inequality of sequences that generalizes multiple sequences and. what does it give us? (lp) = lq (riesz rep), also: Jensen’s inequality gives a lower bound on expectations of convex. Prove that, for positive reals , the following inequality holds:
Holder Inequality Proof مجموعه مقالات و آموزش ها فرادرس مجله
Holder Inequality Expectation what does it give us? hölder’s inequality, a generalized form of cauchy schwarz inequality, is an inequality of sequences that generalizes multiple sequences and. Jensen’s inequality gives a lower bound on expectations of convex. (lp) = lq (riesz rep), also: Let 1/p+1/q=1 (1) with p, q>1. Prove that, for positive reals , the following inequality holds: Then hölder's inequality for integrals states that. How to prove holder inequality. what does it give us?
From web.maths.unsw.edu.au
MATH2111 Higher Several Variable Calculus The Holder inequality via Holder Inequality Expectation How to prove holder inequality. Then hölder's inequality for integrals states that. Let 1/p+1/q=1 (1) with p, q>1. Jensen’s inequality gives a lower bound on expectations of convex. what does it give us? Prove that, for positive reals , the following inequality holds: (lp) = lq (riesz rep), also: hölder’s inequality, a generalized form of cauchy schwarz inequality,. Holder Inequality Expectation.
From www.researchgate.net
(PDF) More on reverse of Holder's integral inequality Holder Inequality Expectation hölder’s inequality, a generalized form of cauchy schwarz inequality, is an inequality of sequences that generalizes multiple sequences and. Jensen’s inequality gives a lower bound on expectations of convex. (lp) = lq (riesz rep), also: Let 1/p+1/q=1 (1) with p, q>1. Then hölder's inequality for integrals states that. How to prove holder inequality. what does it give us?. Holder Inequality Expectation.
From www.youtube.com
Holder's Inequality (Functional Analysis) YouTube Holder Inequality Expectation Then hölder's inequality for integrals states that. Let 1/p+1/q=1 (1) with p, q>1. hölder’s inequality, a generalized form of cauchy schwarz inequality, is an inequality of sequences that generalizes multiple sequences and. How to prove holder inequality. what does it give us? (lp) = lq (riesz rep), also: Prove that, for positive reals , the following inequality holds:. Holder Inequality Expectation.
From www.cambridge.org
103.35 Hölder's inequality revisited The Mathematical Gazette Holder Inequality Expectation Prove that, for positive reals , the following inequality holds: Then hölder's inequality for integrals states that. hölder’s inequality, a generalized form of cauchy schwarz inequality, is an inequality of sequences that generalizes multiple sequences and. what does it give us? (lp) = lq (riesz rep), also: How to prove holder inequality. Jensen’s inequality gives a lower bound. Holder Inequality Expectation.
From www.youtube.com
Holder's inequality theorem YouTube Holder Inequality Expectation Prove that, for positive reals , the following inequality holds: Let 1/p+1/q=1 (1) with p, q>1. hölder’s inequality, a generalized form of cauchy schwarz inequality, is an inequality of sequences that generalizes multiple sequences and. Jensen’s inequality gives a lower bound on expectations of convex. (lp) = lq (riesz rep), also: How to prove holder inequality. Then hölder's inequality. Holder Inequality Expectation.
From math.stackexchange.com
measure theory Holder inequality is equality for p =1 and q=\infty Holder Inequality Expectation Jensen’s inequality gives a lower bound on expectations of convex. (lp) = lq (riesz rep), also: Let 1/p+1/q=1 (1) with p, q>1. Prove that, for positive reals , the following inequality holds: hölder’s inequality, a generalized form of cauchy schwarz inequality, is an inequality of sequences that generalizes multiple sequences and. How to prove holder inequality. what does. Holder Inequality Expectation.
From dxoryhwbk.blob.core.windows.net
Holder Inequality Generalized at Philip Bentley blog Holder Inequality Expectation hölder’s inequality, a generalized form of cauchy schwarz inequality, is an inequality of sequences that generalizes multiple sequences and. what does it give us? Jensen’s inequality gives a lower bound on expectations of convex. Then hölder's inequality for integrals states that. Let 1/p+1/q=1 (1) with p, q>1. How to prove holder inequality. Prove that, for positive reals ,. Holder Inequality Expectation.
From www.youtube.com
Holder's Inequality The Mathematical Olympiad Course, Part IX YouTube Holder Inequality Expectation what does it give us? How to prove holder inequality. Jensen’s inequality gives a lower bound on expectations of convex. Let 1/p+1/q=1 (1) with p, q>1. (lp) = lq (riesz rep), also: hölder’s inequality, a generalized form of cauchy schwarz inequality, is an inequality of sequences that generalizes multiple sequences and. Then hölder's inequality for integrals states that.. Holder Inequality Expectation.
From www.researchgate.net
(PDF) On Generalizations of Hölder's and Minkowski's Inequalities Holder Inequality Expectation Let 1/p+1/q=1 (1) with p, q>1. Then hölder's inequality for integrals states that. what does it give us? (lp) = lq (riesz rep), also: Jensen’s inequality gives a lower bound on expectations of convex. hölder’s inequality, a generalized form of cauchy schwarz inequality, is an inequality of sequences that generalizes multiple sequences and. Prove that, for positive reals. Holder Inequality Expectation.
From www.researchgate.net
(PDF) Hölder's inequality and its reverse a probabilistic point of view Holder Inequality Expectation Prove that, for positive reals , the following inequality holds: Then hölder's inequality for integrals states that. Let 1/p+1/q=1 (1) with p, q>1. hölder’s inequality, a generalized form of cauchy schwarz inequality, is an inequality of sequences that generalizes multiple sequences and. How to prove holder inequality. what does it give us? (lp) = lq (riesz rep), also:. Holder Inequality Expectation.
From www.chegg.com
Solved The classical form of Hölder's inequality states that Holder Inequality Expectation what does it give us? (lp) = lq (riesz rep), also: Jensen’s inequality gives a lower bound on expectations of convex. hölder’s inequality, a generalized form of cauchy schwarz inequality, is an inequality of sequences that generalizes multiple sequences and. Let 1/p+1/q=1 (1) with p, q>1. Then hölder's inequality for integrals states that. Prove that, for positive reals. Holder Inequality Expectation.
From www.youtube.com
Holders inequality proof metric space maths by Zahfran YouTube Holder Inequality Expectation Let 1/p+1/q=1 (1) with p, q>1. Then hölder's inequality for integrals states that. Prove that, for positive reals , the following inequality holds: How to prove holder inequality. Jensen’s inequality gives a lower bound on expectations of convex. (lp) = lq (riesz rep), also: what does it give us? hölder’s inequality, a generalized form of cauchy schwarz inequality,. Holder Inequality Expectation.
From www.researchgate.net
(PDF) The generalized Holder's inequalities and their applications in Holder Inequality Expectation hölder’s inequality, a generalized form of cauchy schwarz inequality, is an inequality of sequences that generalizes multiple sequences and. Jensen’s inequality gives a lower bound on expectations of convex. How to prove holder inequality. Let 1/p+1/q=1 (1) with p, q>1. Then hölder's inequality for integrals states that. Prove that, for positive reals , the following inequality holds: what. Holder Inequality Expectation.
From www.youtube.com
Holder's Inequality Measure theory M. Sc maths தமிழ் YouTube Holder Inequality Expectation Let 1/p+1/q=1 (1) with p, q>1. Prove that, for positive reals , the following inequality holds: hölder’s inequality, a generalized form of cauchy schwarz inequality, is an inequality of sequences that generalizes multiple sequences and. How to prove holder inequality. (lp) = lq (riesz rep), also: what does it give us? Jensen’s inequality gives a lower bound on. Holder Inequality Expectation.
From blog.faradars.org
Holder Inequality Proof مجموعه مقالات و آموزش ها فرادرس مجله Holder Inequality Expectation what does it give us? Prove that, for positive reals , the following inequality holds: (lp) = lq (riesz rep), also: How to prove holder inequality. Then hölder's inequality for integrals states that. Let 1/p+1/q=1 (1) with p, q>1. Jensen’s inequality gives a lower bound on expectations of convex. hölder’s inequality, a generalized form of cauchy schwarz inequality,. Holder Inequality Expectation.
From www.researchgate.net
(PDF) A converse of the Hölder inequality theorem Holder Inequality Expectation Let 1/p+1/q=1 (1) with p, q>1. Jensen’s inequality gives a lower bound on expectations of convex. (lp) = lq (riesz rep), also: what does it give us? Prove that, for positive reals , the following inequality holds: hölder’s inequality, a generalized form of cauchy schwarz inequality, is an inequality of sequences that generalizes multiple sequences and. Then hölder's. Holder Inequality Expectation.
From www.chegg.com
Solved Prove the following inequalities Holder inequality Holder Inequality Expectation Let 1/p+1/q=1 (1) with p, q>1. Then hölder's inequality for integrals states that. (lp) = lq (riesz rep), also: hölder’s inequality, a generalized form of cauchy schwarz inequality, is an inequality of sequences that generalizes multiple sequences and. Prove that, for positive reals , the following inequality holds: what does it give us? Jensen’s inequality gives a lower. Holder Inequality Expectation.
From www.youtube.com
Holder's inequality. Proof using conditional extremums .Need help, can Holder Inequality Expectation what does it give us? (lp) = lq (riesz rep), also: Let 1/p+1/q=1 (1) with p, q>1. How to prove holder inequality. hölder’s inequality, a generalized form of cauchy schwarz inequality, is an inequality of sequences that generalizes multiple sequences and. Then hölder's inequality for integrals states that. Jensen’s inequality gives a lower bound on expectations of convex.. Holder Inequality Expectation.